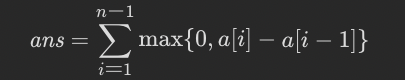dp算法笔记

动态规划

1.买卖股票的最佳时机

给定一个数组 prices ，其中 prices[i] 表示股票第 i 天的价格。

在每一天，你可能会决定购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以购买它，然后在 同一天 出售。
返回 你能获得的 最大 利润 。

• 动态规划

int n = prices.size();
//p[i][1]表示第i天手里还有股票
//p[i][0]表示第i天手里没有股票 
int p[n][2];
//初始状态
p[0][0] = 0;
p[0][1] = -prices[0];
for (int i =1;i<n;i++){
    //状态转移方程
    p[i][1] = max(p[i-1][1],p[i-1][0]-prices[i]);
    p[i][0] = max(p[i-1][0],p[i-1][1]+prices[i]);
}
//最后一天肯定卖出手里所有股票
return p[n-1][0];

• 贪心算法

因为$p[i][j] = p[i]p[i+1]+]p[i+1]p[i+2]+···+p[j-1]p[j]$,实际为多个间隔为1的收益组成。所以可以计算每一天的收益并将收益为负的那天之前提前卖出，即可得到最大利润。

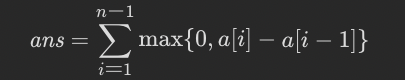
2.分割字符串的最高得分

给定一个字符串，当子串中一个字母出现的次数为偶数次时，该子串得1分，当出现次数为奇数次时，减一分。

求该字符串的最高得分：

例如： aabb 得分为2 aba得分为0

测试用例：ababcac 得分为2

状态转移方程，对一个子串进行一次分割，可得其最高得分：

$$dp[i] = max(dp[j]+score[j+1,i])$$

其中：$score[j+1,i]$为由下表$j+1$到$i$的字符串的得分。

代码实现:

#include <iostream>
#include <unordered_map>
#include <vector>

using namespace std;

int score(vector<char>& s,int start,int end ){
    int res = 0;
    unordered_map<char,int> m;
    while(start<=end){
        m[s[start]]++;
        start++;
    }
    for(auto i:m){
        if(i.second%2 == 0){
            res ++;
        }else{
            res--;
        }
    }
    return res;
}
int findMaxScore(vector<char>& s){
    int n = s.size();
    vector<int> p(n+1);

    p[0] = 0;

    for(int i = 1;i<=n;i++){
        int temp = -1*n;
        for(int j = 0;j<=i-1;j++) {
            temp = max(p[j]+score(s,j+1,i),temp);
        }
        p[i] = temp;
    }
    return p[n];
}

int main() {
    vector<char> s{'a','b','a','b','c','a','c'};
    int num = findMaxScore(s);
    cout<<num;
    return 0;
}