树算法笔记
1.深度优先搜索 DFS
涉及问题: 算法思路较为奇怪 或对空间要求比较高的
- 尽量往深处搜,到了叶节点会回溯
- 使用栈
- 空间 $O(h)$
- 不具有最短性

使用递归写DFS,系统通过隐藏栈完成回溯
注意恢复现场
经典题目:
排列数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include<iostream>
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];
void dfs(int u){
if(u ==n){
for(int i x=0 ;i<n;i++){
cout<<path[i]<<" ";
}
cout<<"\n";
}
if(u!=n){
for(int i = 1;i<=n;i++){
if(!st[i]){
path[u] = i;
st[i] = true;
dfs(u+1);
st[i] = false;
}
}
}
}
int main(){
cin>>n;
dfs(0);
return 0;
}
|
全排列2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <vector>
#include <string>
using namespace std;
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
vector<bool> st;
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(),nums.end());
path = vector<int> (nums.size());
st = vector<bool> (nums.size());
dfs(nums,0);
return res;
}
void dfs(vector<int> & nums, int u){
if(nums.size() == u){
res.push_back(path);
return;
}
for(int i=0;i<nums.size();i++){
if(!st[i]){
if(i&&nums[i-1] == nums[i]&& !st[i-1]) continue;
st[i] = true;
path[u] = nums[i];
dfs(nums,u+1);
st[i] = false;
}
}
}
};
|
2.宽度优先搜索 BFS
涉及问题: 最小步数 最短距离 最少操作次数
- 分别将每一层遍历
- 使用队列
- 空间$O(2^h)$
- 最短路 每次遍历的点是最近的点
3.树与图的存储
4.计算树的最大深度
计算一个二叉树的最大深度:
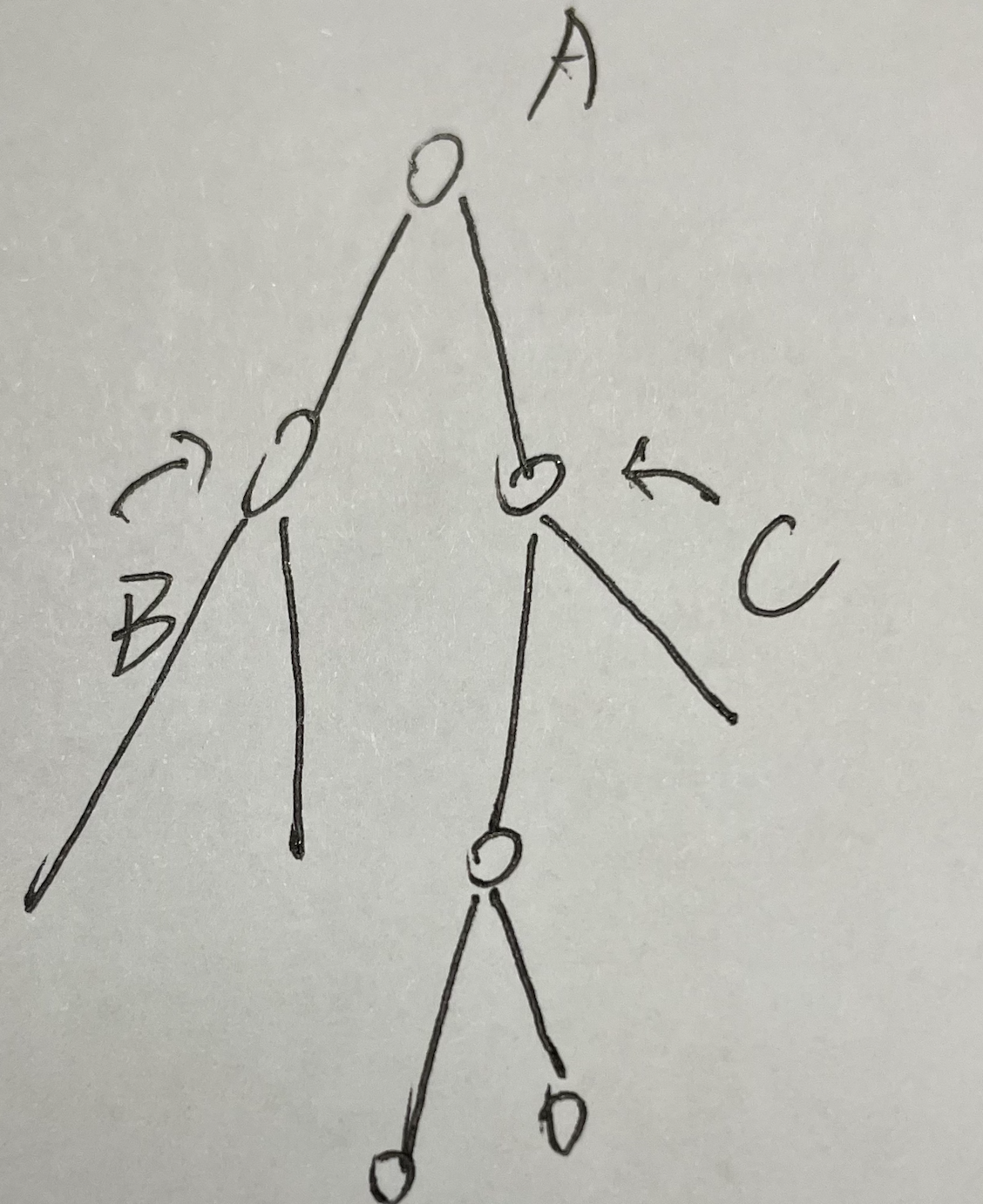
A点到叶子节点的距离为 max(A的左子树B到叶子节点的距离,A的右子树B到叶子节点的距离)+ 1
1
2
3
4
| int maxDepth(TreeNode* root) {
if(!root) return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
|
5.验证二叉搜索树
lc.98

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| bool isValidBST(TreeNode* root) {
if(!root) return true;
vector<int> res = isBST(root);
return res[0]?true:false;
}
vector<int> isBST(TreeNode * root){
vector<int> res({1,root->val,root->val});
if(root->left){
vector<int> t = isBST(root->left);
if(!t[0]||t[2]>=root->val){
res[0] = 0;
}
res[1] = min(res[1],t[1]);
res[2] = max(res[2],t[2]);
}
if(root->right){
vector<int> t = isBST(root->right);
if(!t[0]||t[1]<=root->val){
res[0] = 0;
}
res[1] = min(res[1],t[1]);
res[2] = max(res[2],t[2]);
}
return res;
}
|
中序遍历得到一个有序数组即为二叉搜索树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| long pre = LONG_MIN;
bool isValidBST(TreeNode* root) {
return isBST(root);
}
bool isBST(TreeNode* root){
if(!root) return 1;
bool l = isBST(root->left);
if(root->val <= pre) return 0;
pre = root->val;
bool r = isBST(root->right);
return l&&r;
}
|
6.对称二叉树
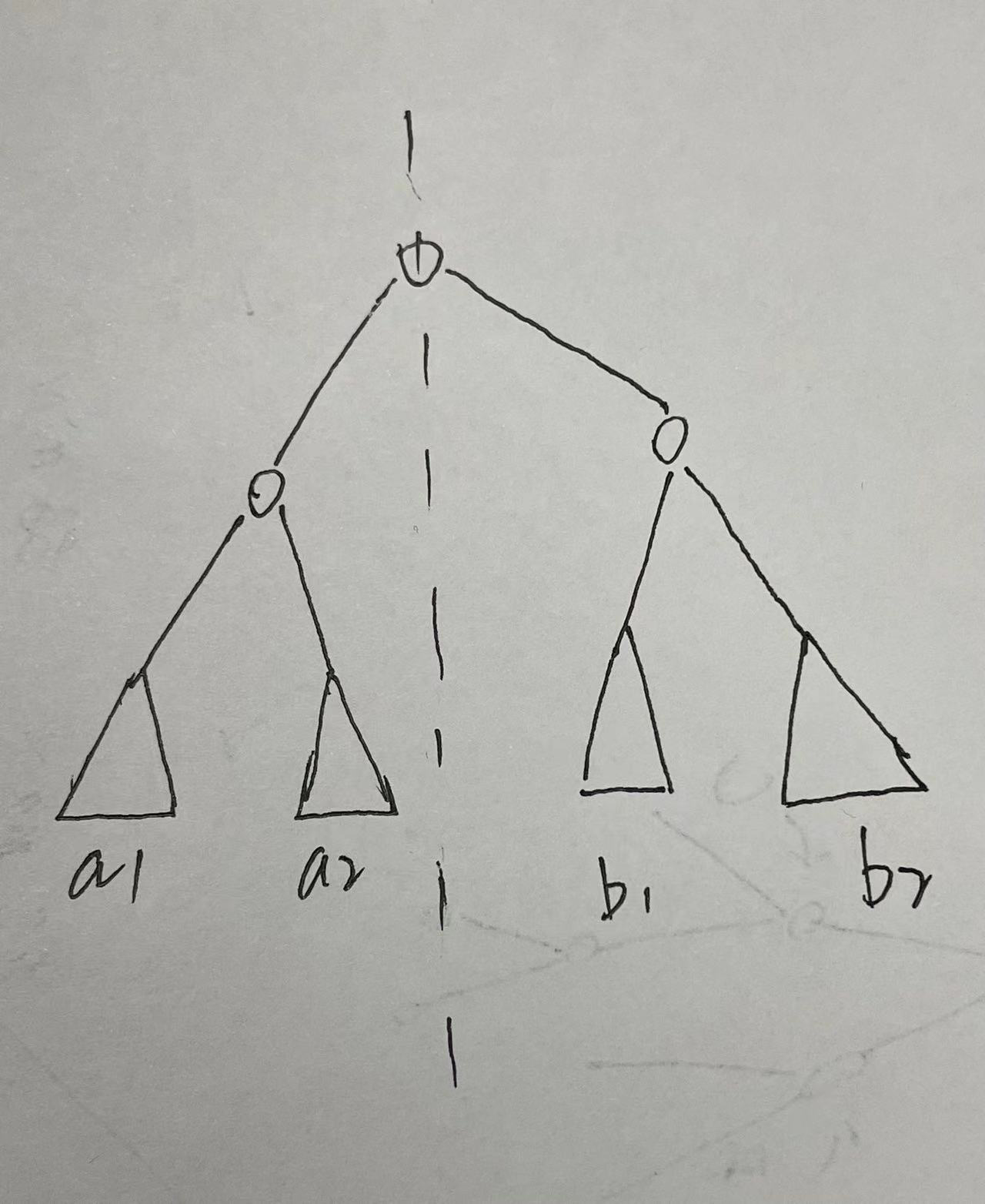
只需验证:
- 左子树根节点与右子树根节点是否相同
- 左子树的左子树与右子树的右子树是否相同
- 左子树的右子树与右子树的左子树是否相同
1
2
3
4
5
6
7
8
9
10
11
| bool isSymmetric(TreeNode* root) {
if(!root) return true;
return isSym(root->left,root->right);
}
bool isSym(TreeNode * rootleft,TreeNode * rootright){
if(!rootleft&&!rootright) return true;
if(!rootleft||!rootright||rootleft->val!=rootright->val) return false;
return isSym(rootleft->right,rootright->left)&&isSym(rootleft->left,rootright->right);
}
|





