FisherYu626

一颗有趣的灵魂~

0%

数组类算法笔记2

发表于 更新于 分类于
本文字数： 10k 阅读时长 ≈ 9 分钟

数组类算法笔记2

1.寻找数组的中心索引

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

  • 遍历整个数组，分别计算中轴两侧数值和是否相等。(计算量大，每次需要计算两边数组的和，超时)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int pivotIndex(vector<int> &nums)
    {
        int pivot;
        for(pivot =0;pivot<nums.size();pivot ++){
            if(sum(nums,0,pivot-1) == sum(nums,pivot+1,nums.size()-1)){
                return pivot;
            }
        }
        return -1; 
    }
    int sum(vector<int> &nums,int left,int right)
    {
        int res = 0;
        if (right == -1 || left == nums.size()) return res;
        for (int i = left;i<=right;i++){
            res += nums[i];
        }
        return res;
    }

  • 先计算整个数组的和，删去中轴元素即为右侧和，比较当前左侧和右侧和是否相等，不相等则给左侧和加上删去的数，进行下一次遍历。

    减少了重复计算的工作量，不需要每次循环都计算左右两侧的元素和。

    1. 先求得数组中所有元素之和sum；

    2. 遍历数组，取当前下标左边的元素之和left_sum，同时sum减去已遍历元素，比较二者是否相等，相等则返回当前下标；

    3. 遍历结束，代表没有中心索引，返回-1；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int pivotIndex(vector<int> &nums)
    {
        int sum = 0;
        int lsum = 0;//中轴元素左侧元素之和
        for (int i = 0;i<nums.size();i++){
            sum += nums[i];
        }
        for (int pivot = 0; pivot <nums.size();pivot++){
            sum -= nums[pivot];
            if(lsum == sum) return pivot;
            lsum += nums[pivot];
        }
        return -1;
    }

2.搜索数组插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

  • 最简单的思路

    1. 如果数组中的值大于或者等于target，直接return
    2. 如果全部遍历完证明target是最大的数，直接插入末尾
    1
    2
    3
    4
    5
    6
    7
    int searchInsert(vector<int> &nums, int target)
        {
            for (int i = 0;i<nums.size();i++){
                if (nums[i]>=target) return i;
            }
            return nums.size();
        }

  • 二分查找，

    前提是查找的数组是一个有序数组。如果二分查找没有找到结果，则left所在位置即为查找数字的期望所在位置！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int searchInsert(vector<int> &nums, int target)
    {
        int right = nums.size() - 1;
        int left = 0;
        int mid;
        while (left <= right)
        {
            mid = (left + right) / 2;
            if (nums[mid] == target)
                return mid;
            if (nums[mid] < target)
            {
                left = mid + 1;
            }
            else
            {
                right = mid - 1;
            }
        }
        return left;
    }

3.合并数组

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

返回vector的最后一个元素的引用 vec.back()

思路：首先，我们将列表中的区间按照左端点升序排序。然后我们将第一个区间加入 merged 数组中，并按顺序依次考虑之后的每个区间：

如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后，那么它们不会重合，我们可以直接将这个区间加入数组 merged 的末尾；

否则，它们重合，我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点，将其置为二者的较大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(),intervals.end());
        int l,r;
        l = intervals[0][0];
        r = intervals[0][1];
        res.push_back(intervals[0]);
        for(int i = 1;i<intervals.size();i++){ //size()返回的是二维数组中元素的个数
            if(r<intervals[i][0]){
                l = intervals[i][0];
                r = intervals[i][1];
                res.push_back({l,r});
            }else{
                res.back()[1] = max(r,intervals[i][1]); //Returns a read/write reference to the data at the last element of the vector.
                r = res.back()[1];
            }
        } 
        return res;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(),intervals.end());
        for (int i = 0;i<intervals.size();i++){
            int l = intervals[i][0];
            int r = intervals[i][1];
            if(!res.size() || res.back()[1]<l){
                res.push_back({l,r});
            }else{
                res.back()[1] = max(r,res.back()[1]);
            }
        }
        return res;
    }

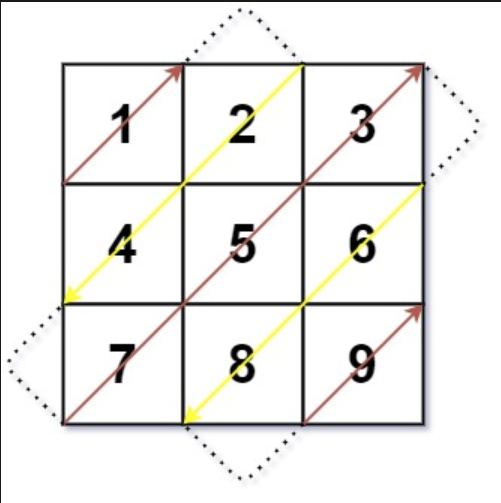
4.二维数组 对角线遍历

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

image-20220301205651422

思路：

设元素当前行列坐标为(x,y),元素如果下一次要向左下移动(x+1, y-1)和右上移动(x-1, y+1)的话，并不会改变当前(行 + 列)的和;
if (x + y)是偶数, 那么下一次就是往右上移动, 是奇数的话下一次就是往左下移动；
左下 = [x+1, y-1]:
如果在最后一行 => 向右 x+0, y+1;
如果在第一列 => 向下 [x+1, y+0];
右上 = [x-1, y+1]:
如果在最后一列 => 向下 x+1, y+0;
如果在第一行 => 向右 [x+0, y+1];

注意：左上右下的顺序各自有区分！！

  • 第一列也可以在最后一行，但最后一行的第一列必须向右（左下角）
  • 最后一列也可以在第一行，但第一行的最后一列只能向下（右上角）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        vector<int> res;
        int row = mat.size();
        int col = mat[0].size();
        int n = row*col;
        int x = 0;
        int y = 0;
        for(int i = 0;i<n;i++){
            res.push_back(mat[x][y]);
            if((x+y)%2 == 0){
                if(y == col-1){
                    x++;
                }else if(x == 0){
                    y++;
                }else{
                    x--;
                    y++;
                }
            }else{
                if(x == row-1){
                    y++;
                }else if(y == 0){
                    x++;
                }else{
                    x++;
                    y--;
                }
            }
        }
        return res;
    }

5.最长回文字符串

给你一个字符串 s，找到 s 中最长的回文子串。

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
string longestPalindrome(string s) {
        //长度为0或仅一个字符 为回文字符串 返回
        if(s.length()<2){
            return s;
        }
        int maxlen = 1;
        int n = s.length();
        int flag = 0;
        vector<vector<int>> dp(n,vector<int> (n));
        //单个字符为回文串 作为dp的最基本单元
        for(int i = 0;i<n;i++){
            dp[i][i] = 1;
        }
        for(int L = 2;L<=n;L++){
            for(int i = 0;i<n;i++){
                int j  = i + L - 1;
                if(j>=n) break;
                if(s[i] != s[j]){
                    dp[i][j] = 0;
                }else{
                    if(j-i<3){
                        dp[i][j] = 1;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }
                }
                if(dp[i][j]&&(j-i+1)>maxlen){
                    maxlen = j-i+1;
                    flag = i;
                }
            }
        }
        return s.substr(flag,maxlen);
    }

中心扩展算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
string longestPalindrome(string s) {
        int start = 0;
        int end = 0;
        int n = s.length();
        int len,len1,len2;
        for(int i = 0;i<n;i++){
            len1 = expandCenter(s,i,i);
            len2 = expandCenter(s,i,i+1);
            len = max(len1,len2);

            if(len>end-start+1){
                start = i - (len-1)/2;
                end = i + len/2;
            }
        }
        return s.substr(start,end-start+1);
    }
    int expandCenter(string s,int left,int right){
        while(left>=0&&right<s.length()&&s[left] == s[right]){
            left--;
            right++;
        }
        return right-left-1;
    }

6.拆分数组1

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), …, (an, bn) ，使得从 1 到 n 的 min(ai, bi) 总和最大。

返回该 最大总和

  • 思路：先排序 后求和

采用快排

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int arrayPairSum(vector<int>& nums) {
    int sum = 0;
    QuickSort(nums,0,nums.size()-1);
    for(int i = 0;i<nums.size();i+=2){
        sum+=nums[i];
    }
    return sum;
}
void QuickSort(vector<int>& nums,int left,int right){
    if(left<right){
        int pos = Parition(nums,left,right);
        QuickSort(nums,left,pos-1);
        QuickSort(nums,pos+1,right);
    }
    return;
}
int Parition(vector<int>& nums,int left,int right){
    int temp = nums[left];
    while(left<right){
        while(left<right && nums[right]>temp)right--;
        nums[left] = nums[right];
        //注意快排下式的等号 如果没有这个<=的=，就会进入死循环！！ 6,6,5,2,1,3
        while(left<right && nums[left]<=temp) left++;
        nums[right] = nums[left];
    }
    nums[left] = temp;
    return left;
}

7.杨辉三角2

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

image-20220308153029722

image-20220308152002493

基于公式$C^in =C^{i-1}{n-1}+C^i_{n-1}$

$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<vector<int>> num(rowIndex+1);
        for(int i = 0;i<rowIndex+1;i++){
            num[i].resize(i+1);
            num[i][0] = num[i][i] = 1;
            for(int j = 1;j<i;j++){
                num[i][j] = num[i-1][j-1]+num[i-1][j];
            }
        }
        return num[rowIndex];
    }
};

递归 超过$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
vector<int> getRow(int rowIndex) {
        vector<int> num(rowIndex+1);
        for(int i = 0;i<rowIndex+1;i++){
            num[i] = triangle(rowIndex,i);
        }
        return num;
    }
    int triangle(int rowIndex,int i){
        if (i == 0 ||i==rowIndex) return 1;
        return triangle(rowIndex-1,i-1)+triangle(rowIndex-1,i);
    }

递推式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> pre, cur;
        for (int i = 0; i <= rowIndex; ++i) {
            cur.resize(i + 1);
            cur[0] = cur[i] = 1;
            for (int j = 1; j < i; ++j) {
                cur[j] = pre[j - 1] + pre[j];
            }
            pre = cur;
        }
        return pre;
    }
};

将空间复杂度2n降到n,倒着计算当前行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> row(rowIndex + 1);
        row[0] = 1;
        for (int i = 1; i <= rowIndex; ++i) {
            for (int j = i; j > 0; --j) {
                row[j] += row[j - 1];
            }
        }
        return row;
    }
};

时间复杂度$O(rowIndex)$做法 以下拷贝官方解 官方解有问题

image-20220308152827899

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> row(rowIndex + 1);
        row[0] = 1;
        for (int i = 1; i <= rowIndex; ++i) {
            row[i] = 1LL * row[i - 1] * (rowIndex - i + 1) / i;
        }
        return row;
    }
};

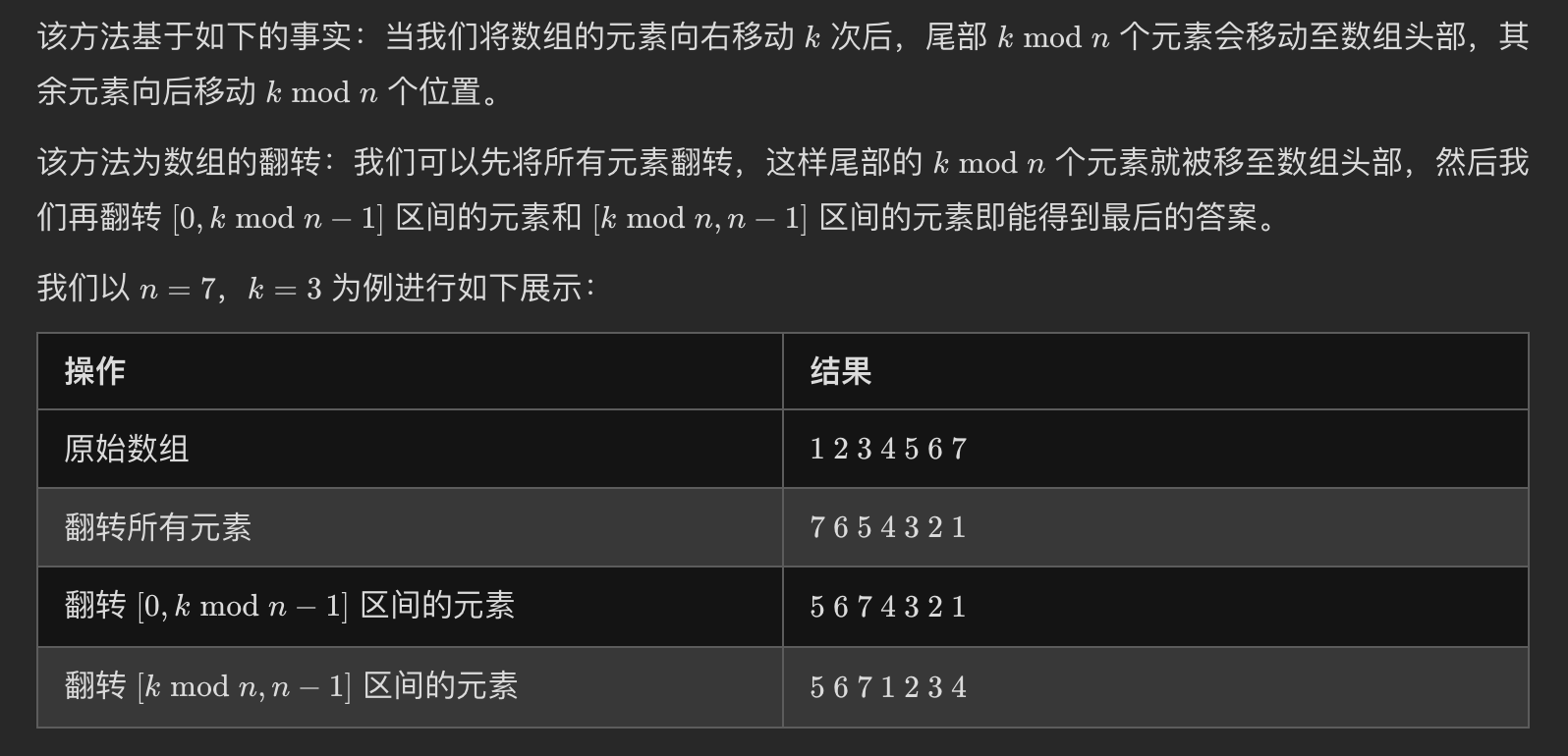
8.轮转数组

  • 使用临时空间

image-20220318152902508

image-20220318152911180

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int n = nums.size();
if(k == n) return;
if(k>n) k = k%n;
vector<int> temp(k);
int j = 0;
for (int i = 0;i<k;i++){
    temp[k-1-i] = nums[n-1-i];
}
for(int i = n-1-k;i>=0;i--){
    nums[n-1-j] = nums[i];
    j++;
}
for(int i = 0;i<k;i++){
    nums[i] = temp[i];
}
return;
  • 翻转image-20220318152957859

9.只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

位运算：

image-20220320103737882

image-20220320103755119

10.两个数组的交集

给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。

  • hash表 时间$O(n+m)$ 空间$O(min(n,m))$

由于同一个数字在两个数组中都可能出现多次，因此需要用哈希表存储每个数字出现的次数。对于一个数字，其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。

首先遍历第一个数组，并在哈希表中记录第一个数组中的每个数字以及对应出现的次数，然后遍历第二个数组，对于第二个数组中的每个数字，如果在哈希表中存在这个数字，则将该数字添加到答案，并减少哈希表中该数字出现的次数。

为了降低空间复杂度，首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数，然后遍历较长的数组得到交集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if(nums1.size()>nums2.size()){
            return intersect(nums2,nums1);
        }
        unordered_map<int,int> m;
        vector<int> res;
        for(int i = 0;i<nums1.size();i++){
            m[nums1[i]]++;
        }
        for(int j = 0;j<nums2.size();j++){
            if(m.count(nums2[j])&&m[nums2[j]]>0) {
                m[nums2[j]] --;
                res.push_back(nums2[j]);
            }
       }
        return res;
    }
  • 双指针 时间$O(nlogn+mlogm)$ 空间$O(1)$

如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

首先对两个数组进行排序，然后使用两个指针遍历两个数组。

初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
vector<int> intersect(vector<int> &nums1, vector<int> &nums2)
{
    int n = nums1.size();
    int m = nums2.size();
    vector<int> res;
    int i = 0, j = 0;
    sort(nums1.begin(),nums1.end());
    sort(nums2.begin(),nums2.end());
    while (i < n && j < m)
    {
        if (nums1[i] == nums2[j])
        {
            res.push_back(nums1[i]);
            i++;
            j++;
        }
        else if (nums1[i] < nums2[j])
        {
            i++;
        }
        else
        {
            j++;
        }
    }
    return res;
}

12.二分查找

1
2
3
4
5
6
7
8
9
10
11
12
int search(vector<int>& nums, int target) {
        int low = 0;
        int high = nums.size()-1;
        int mid = (low+high)/2;
        while(low <= high){
            if(nums[mid] == target) return mid;
            if(nums[mid]<target) low = mid+1;
            if(nums[mid]>target) high = mid-1;
            mid = (high+low)/2;
        }
        return -1;
    }

13.螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res;
        int n = matrix.size();
        int m = matrix[0].size();
  			//方向矩阵
        int dx[] = {0,1,0,-1},dy[] = {1,0,-1,0};
 				//记录当前位置是否遍历过 遍历过则换方向
        vector<vector<bool>> st(n,vector<bool> (m));
        
        for(int i =0,x=0,y=0,d=0;i<m*n;i++){
            res.push_back(matrix[x][y]);
            st[x][y] = true;
            
            int a = x+dx[d],b = y+dy[d];
          //越界或已经遍历则换方向
            if(a<0||a>=n||b<0||b>=m||st[a][b]){
                d = (d+1)%4;
                a = x+dx[d];
                b = y+dy[d];
            }
            x = a;
            y = b;
        }
        return res;
    }