数组类算法笔记(双指针)
数组类算法笔记(双指针)
1.两数之和 II - 输入有序数组
给定一个已按照 非递减顺序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
1 | 输入:numbers = [2,7,11,15], target = 9 |
暴力解法 时间复杂度O(n^2)
unordered_map
unoered_map底层由哈希表实现,索引的查找时间复杂度为O(1),利用这个性质,一层循环即可实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution
{
public:
unordered_map<int, int> m;
vector<int> twoSum(vector<int> &numbers, int target)
{
for (int i = 0; i < numbers.size(); i++)
{
if (m.count(target - numbers[i]))
{
return {m.at(target - numbers[i]), i + 1};
}
else
{
m.emplace(numbers[i], i + 1);
}
}
return {};
}
};对撞指针
两个指针分别指向最小最大数,并不断向中间靠拢。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution
{
public:
vector<int> twoSum(vector<int> &numbers, int target)
{
int n = numbers.size() - 1;
int i = 0;
while (i < n)
{
if (numbers[i] + numbers[n] == target)
{
return {i + 1, n + 1};
}
else if (numbers[i] + numbers[n] < target)
{
i++;
}
else if (numbers[i] + numbers[n] > target)
{
n--;
}
}
return {};
}
};
2.验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
isalnum()判断一个字符是否是字母或数字
int isalnum ( int c );
isalnum() 函数用来检测一个字符是否是字母或者十进制数字。
如果仅仅检测一个字符是否是字母,可以使用 isalpha() 函数;如果仅仅检测一个字符是否是十进制数字,可以使用 isdigit() 函数。
如果一个字符被 isalpha() 或者 isdigit() 检测后返回“真”,那么它被 isalnum() 检测后也一定会返回“真”。
标准 ASCII 编码共包含了 128 个字符,不同的字符属于不同的分类,我们在 [ctype.h](http://c.biancheng.net/ref/ctype_h/) 头文件中给出了详细的列表。
1
2
3
4
5示例 1:
输入: "A man, a plan, a canal: Panama"
输出: true
解释:"amanaplanacanalpanama" 是回文串
3.长度最小的子数组
暴力破解法
时间复杂度 $O(n^2)$,从头到尾遍历所有满足>=target的子数组,并将最短长度返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17int minSubArrayLen(int target, vector<int>& nums) {
int i = 0;
int j ;
int sum;
int length = nums.size()+1;
for (int i = 0;i<nums.size();i++){
sum = nums[i];
if(sum>=target) return 1;
for (j=i+1;j<nums.size();j++){
sum += nums[j];
if(sum>=target&&(j-i+1)<length){
length = j - i + 1;
}
}
}
return length==nums.size()+1?0:length;
}滑动窗口法
减少了每次重新定位右侧边界的时间。先不断增大右侧边界以达到target,再不断缩减左侧边界以保证最小长度。近遍历一次数组并随时存储满足target的最小长度。
时间复杂度$O(2n)$,空间复杂度$O(1)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17int minSubArrayLen(int target, vector<int>& nums) {
int i = 0;
int j = 0;
int sum = 0;
int length = nums.size()+1;
while (j<nums.size())
{
sum += nums[j];
while(sum >= target){
length = min(length,j-i+1);
sum -= nums[i];
i++;
}
j++;
}
return length==nums.size()+1?0:length;
}
4.二维数组 旋转矩阵
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?

- 借助辅助矩阵 (空间复杂度 $O(N^2)$)
1 | void rotate(vector<vector<int>>& matrix) { |
每次旋转4个位置 空间复杂度$O(1)$


关键变换:
代入4次:
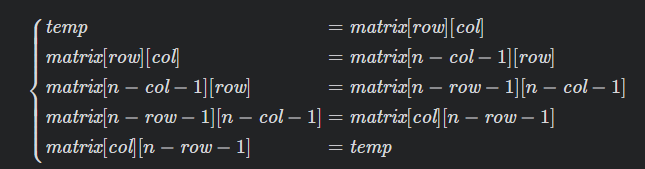
1 | void rotate(vector<vector<int>>& matrix) { |
- 对称2次 空间复杂度$O(1)$
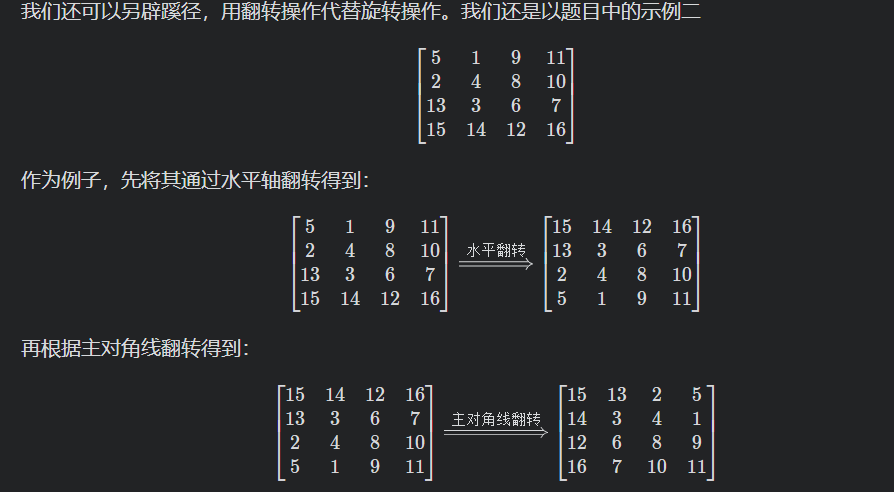

1 | void rotate(vector<vector<int>>& matrix) { |
5.零矩阵
编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
- 空间复杂度$O(n^2)$
1 | class Solution { |
空间复杂度$O(1)$ 2个存储空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41void setZeroes(vector<vector<int>>& matrix) {
int n = matrix.size();
int m = matrix[0].size();
int row = 0;
int col = 0;
for(int i = 0;i<n;i++){
if(!matrix[i][0]){
row = 1;
}
}
for(int j = 0;j<m;j++){
if(!matrix[0][j]){
col = 1;
}
}
for(int i = 1;i<n;i++){
for(int j = 1;j<m;j++){
if(!matrix[i][j]){
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
for(int i = 1;i<n;i++){
for(int j = 1;j<m;j++){
if((!matrix[0][j])||(!matrix[i][0])){
matrix[i][j] = 0;
}
}
}
if(row){
for(int i =0;i<n;i++){
matrix[i][0] = 0;
}
}
if(col){
for(int j = 0;j<m;j++){
matrix[0][j] = 0;
}
}
}
空间复杂度$O(1)$ 1个存储空间
1 | void setZeroes(vector<vector<int>>& matrix) { |